Acceso a ECCOv4 por medio de EarthData in the Cloud de la NASA

Este tutorial demuestra acceso al producto ECCOv4 de un modelo numerico global. Para mayor informacion del producto de ECCO, puede ir aqui.

Requisitos

1. Tener una cuenta de Earth Data Login por medio de la NASA.

2. Tener un Token valido.

Tambien se puede utilizar el metodo de Nombre de Usuario / Contrasena descrito en el tutorial de Autenticacion

Objectivos

Utilizar pydap para demostrar

• Acceso to archivos cientificos de la NASA por medio del uso de tokens y EarthData como metodo de autenticacion.

Algunas variables de interes son:

• Native grid

• Temperature and Salinity

Autor: Miguel Jimenez-Urias, ‘24

import matplotlib.pyplot as plt
import numpy as np
from pydap.net import create_session
from pydap.client import open_url
import xarray as xr
import pydap

print("xarray version: ", xr.__version__)
print("pydap version: ", pydap.__version__)

xarray version:  2025.9.0
pydap version:  3.5.8

Acceso a EARTHDATA

El listado de las variables de este producto pueden encontrarse aqui. En este caso, accederemos a las variables en su malla original, el LL90.

Grid_url = 'https://opendap.earthdata.nasa.gov/providers/POCLOUD/collections/ECCO%20Geometry%20Parameters%20for%20the%20Lat-Lon-Cap%2090%20(llc90)%20Native%20Model%20Grid%20(Version%204%20Release%204)/granules/GRID_GEOMETRY_ECCO_V4r4_native_llc0090'

Autenticacion via .netrc

Las credenciales son recuperadas automaticamente por pydap.

my_session = create_session()

Alternativa: El use the tokens

session_extra = {"token": "YourToken"}

# initialize a requests.session object with the token headers. All handled by pydap.
my_session = create_session(session_kwargs=session_extra)

Accesso a los metadatos solamente, por medio de pydap

pydap aprovecha el protocolo de OPeNDAP, el cual permite la separacion de los metadatos de los valores numericos. Esto permite una inspeccion remota de los datasets.

ds_grid = open_url(Grid_url, session=my_session, protocol="dap4")

ds_grid.tree()

.GRID_GEOMETRY_ECCO_V4r4_native_llc0090.nc
├──dxC
├──PHrefF
├──XG
├──dyG
├──rA
├──hFacS
├──Zp1
├──Zl
├──rAw
├──dxG
├──maskW
├──YC
├──XC
├──maskS
├──YG
├──hFacC
├──drC
├──drF
├──XC_bnds
├──Zu
├──Z_bnds
├──YC_bnds
├──PHrefC
├──rAs
├──Depth
├──dyC
├──SN
├──rAz
├──maskC
├──CS
├──hFacW
├──Z
├──i
├──i_g
├──j
├──j_g
├──k
├──k_l
├──k_p1
├──k_u
├──nb
├──nv
└──tile

Note

PyDAP accesa solo a los metadatos de archivo en el servidor de OPeNDAP, y ningun arreglo numerico ha sido descargardo hasta este punto!

Para descargar los arreglos numericos hay que indexar la variable

Esto es, de la siguiente manera:

# this fetches remote data into a pydap object container
pydap_Array = dataset[<VarName>][:]

donde <VarName> es el nombre de una de las variables. El producto sera una representation “en memoria” de tipo pydap.model.BaseType, el cual permite el acceso a los arreglos de numpy.

Para extraer los valores de la variable remota, hay que ejecutar el siguiente comando

# The `.data` command allows direct access to the Numpy array (e.g. for manipulation)
pydap_Array.data

# lets download some data
Depth = ds_grid['Depth'][:]
print(type(Depth))

<class 'pydap.model.BaseType'>

Depth.attributes

{'_FillValue': 9.969209968e+36,
 'long_name': 'model seafloor depth below ocean surface at rest',
 'units': 'm',
 'coordinate': 'XC YC',
 'coverage_content_type': 'modelResult',
 'standard_name': 'sea_floor_depth_below_geoid',
 'comment': "Model sea surface height (SSH) of 0m corresponds to an ocean surface at rest relative to the geoid. Depth corresponds to seafloor depth below geoid. Note: the MITgcm used by ECCO V4r4 implements 'partial cells' so the actual model seafloor depth may differ from the seafloor depth provided by the input bathymetry file.",
 'coordinates': 'YC XC',
 'origname': 'Depth',
 'fullnamepath': '/Depth',
 'Maps': (),
 '_DAP4_Checksum_CRC32': np.uint32(3811813944)}

Depth.shape, Depth.dims

((13, 90, 90), ['/tile', '/j', '/i'])

Visualizando el fondo oceanico Depth en la malla original del modelo

En este caso, el producto ECCO esta definido en una malla con topologia de un Cubo Esferico. De esta manera, la malla horizontal contiene una dimension extra llamada: tile o face. A continuacion visualizamos la variable en su topologia original

Variable = [Depth[i].data for i in range(13)]
clevels =  np.linspace(0, 6000, 100)
cMap = 'Greys_r'

fig, axes = plt.subplots(nrows=5, ncols=5, figsize=(8, 8), gridspec_kw={'hspace':0.01, 'wspace':0.01})
AXES = [
    axes[4, 0], axes[3, 0], axes[2, 0], axes[4, 1], axes[3, 1], axes[2, 1],
    axes[1, 1], 
    axes[1, 2], axes[1, 3], axes[1, 4], axes[0, 2], axes[0, 3], axes[0, 4],
]
for i in range(len(AXES)):
    AXES[i].contourf(Variable[i], clevels, cmap=cMap)

for ax in np.ravel(axes):
    ax.axis('off')
    plt.setp(ax.get_xticklabels(), visible=False)
    plt.setp(ax.get_yticklabels(), visible=False)

plt.show()

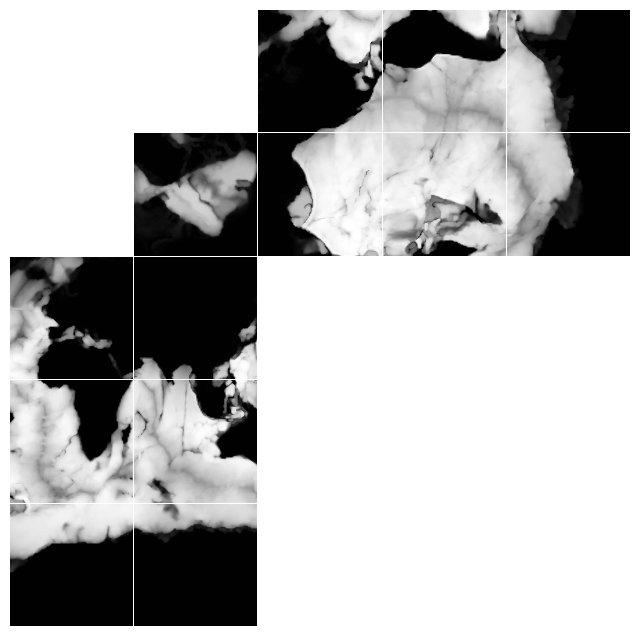
Fig. 1. La variable Depth visualizada en una malla horitonzal. Tiles con valores 0-5 tienen un ordenamiento de valores (indiciales) C-ordering, mientras que cualquier arreglo numerico tiles 7-13 siguen el F-ordering. Cualquier arreglo numerico en el arctic cap, tiene un comportamiento de una coordenada polar.

Visualizacion con topologia corregida

fig, axes = plt.subplots(nrows=4, ncols=4, figsize=(8, 8), gridspec_kw={'hspace':0.01, 'wspace':0.01})
AXES_NR = [
    axes[3, 0], axes[2, 0], axes[1, 0], axes[3, 1], axes[2, 1], axes[1, 1],
]
AXES_CAP = [axes[0, 0]]
AXES_R = [
    axes[1, 2], axes[2, 2], axes[3, 2], axes[1, 3], axes[2, 3], axes[3, 3],
]
for i in range(len(AXES_NR)):
    AXES_NR[i].contourf(Variable[i], clevels, cmap=cMap)

for i in range(len(AXES_CAP)):
    AXES_CAP[i].contourf(Variable[6].transpose()[:, ::-1], clevels, cmap=cMap)

for i in range(len(AXES_R)):
    AXES_R[i].contourf(Variable[7+i].transpose()[::-1, :], clevels, cmap=cMap)

for ax in np.ravel(axes):
    ax.axis('off')
    plt.setp(ax.get_xticklabels(), visible=False)
    plt.setp(ax.get_yticklabels(), visible=False)

plt.show()

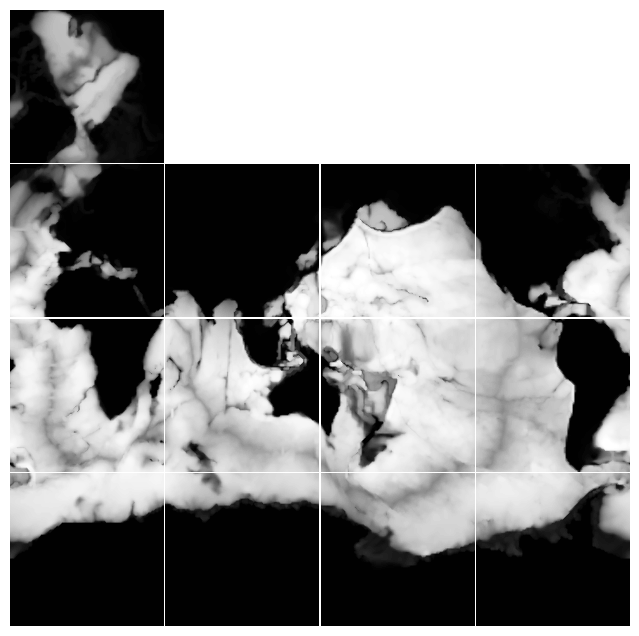
Fig. 2. Visualizacion de la variable Depth en una malla horizontal que approxima una malla horizontal uniforme con ejes lat-lon. Sin embargo, cualquier arreglo numerico en el arctic cap, continua en una malla que approxima una malla en coordenadas polares

Utilizando xarray

pydap se puede llamar dentro de xarray para acceder a los archivos expuestos mediante el servidor de OPeNDAP. En particular, xarray permite aggregar multiples archivos remotos de opendap. A continuacion demostramos un pequeno ejemplo.

Un URL individual –> un archivo remoto

Below we access remote Temperature and Salinity ECCO data with xarray via (internally) pydap.

baseURL = 'https://opendap.earthdata.nasa.gov/providers/POCLOUD/collections/'
Temp_Salt = "ECCO%20Ocean%20Temperature%20and%20Salinity%20-%20Monthly%20Mean%20llc90%20Grid%20(Version%204%20Release%204)/granules/OCEAN_TEMPERATURE_SALINITY_mon_mean_"
year = '2017-'
month = '01'
end_ = '_ECCO_V4r4_native_llc0090'
Temp_2017 = baseURL + Temp_Salt +year  + month + end_

# Convertimos el URL en un DAP4 opendap url
Temp_2017 = Temp_2017.replace("https", "dap4")
Temp_2017

'dap4://opendap.earthdata.nasa.gov/providers/POCLOUD/collections/ECCO%20Ocean%20Temperature%20and%20Salinity%20-%20Monthly%20Mean%20llc90%20Grid%20(Version%204%20Release%204)/granules/OCEAN_TEMPERATURE_SALINITY_mon_mean_2017-01_ECCO_V4r4_native_llc0090'

pyds = open_url(Temp_2017, session=my_session)
pyds.tree()

.OCEAN_TEMPERATURE_SALINITY_mon_mean_2017-01_ECCO_V4r4_native_llc0090.nc
├──XG
├──Zp1
├──Zl
├──YC
├──XC
├──SALT
├──YG
├──XC_bnds
├──Zu
├──THETA
├──Z_bnds
├──YC_bnds
├──time_bnds
├──Z
├──i
├──i_g
├──j
├──j_g
├──k
├──k_l
├──k_p1
├──k_u
├──nb
├──nv
├──tile
└──time

Para evitar descargas variables que no sean necesariamente de interest, se le puede instruir al Servidor Hyrax que variables requiere uno.

Para esto utilizaremos las Expresiones de Restriccion (CE, por sus siglas en ingles). Este metodo nos ayudara a construir datasets mucho mas simples, y evitar descargar N veces, informacion que no es requerida.

A continuacion demostramos el caso de solo requerir la variable THETA y sus dimensiones.

dims = pyds['/THETA'].dims
Vars = ['/THETA'] + dims

# Below construct Contraint Expression
CE = "?dap4.ce="+(";").join(Vars)
print("Constraint Expression: ", CE)

Constraint Expression:  ?dap4.ce=/THETA;/time;/k;/tile;/j;/i

Temp_2017 = baseURL + Temp_Salt +year  + month + end_ + CE
Temp_2017

'https://opendap.earthdata.nasa.gov/providers/POCLOUD/collections/ECCO%20Ocean%20Temperature%20and%20Salinity%20-%20Monthly%20Mean%20llc90%20Grid%20(Version%204%20Release%204)/granules/OCEAN_TEMPERATURE_SALINITY_mon_mean_2017-01_ECCO_V4r4_native_llc0090?dap4.ce=/THETA;/time;/k;/tile;/j;/i'

Importante

Ahora aplicamos la CE a todos los possibles URLs the nuestro dataset.

Temp_2017 = [baseURL.replace("https", "dap4") + Temp_Salt + year + f'{i:02}' + end_ + CE for i in range(1, 13)]
Temp_2017[:3]

['dap4://opendap.earthdata.nasa.gov/providers/POCLOUD/collections/ECCO%20Ocean%20Temperature%20and%20Salinity%20-%20Monthly%20Mean%20llc90%20Grid%20(Version%204%20Release%204)/granules/OCEAN_TEMPERATURE_SALINITY_mon_mean_2017-01_ECCO_V4r4_native_llc0090?dap4.ce=/THETA;/time;/k;/tile;/j;/i',
 'dap4://opendap.earthdata.nasa.gov/providers/POCLOUD/collections/ECCO%20Ocean%20Temperature%20and%20Salinity%20-%20Monthly%20Mean%20llc90%20Grid%20(Version%204%20Release%204)/granules/OCEAN_TEMPERATURE_SALINITY_mon_mean_2017-02_ECCO_V4r4_native_llc0090?dap4.ce=/THETA;/time;/k;/tile;/j;/i',
 'dap4://opendap.earthdata.nasa.gov/providers/POCLOUD/collections/ECCO%20Ocean%20Temperature%20and%20Salinity%20-%20Monthly%20Mean%20llc90%20Grid%20(Version%204%20Release%204)/granules/OCEAN_TEMPERATURE_SALINITY_mon_mean_2017-03_ECCO_V4r4_native_llc0090?dap4.ce=/THETA;/time;/k;/tile;/j;/i']

Debajo inicializaremos una session que persista, cada vez que descargue datos de servidores de OPeNDAP. En este caso utilizaremost la libraria requests_cache. El comportamiento es casi identico excepto la siguiente celda:

cache_session = create_session(use_cache=True, cache_kwargs={"cache_name":"data/ecco"}) # caching the session
cache_session.cache.clear() # clear all cache to demonstrate the behavior

Warning

A partir de la version de pydap >= 3.5.5, existe el nuevo metodo experimental consolidated_metadata que permite a pydap descargar todos los metadatos, y reusarlos. Este metodo continua en desarrollo y sus propiedades pueden cambiar en las siguientes versiones.

from pydap.client import consolidate_metadata

%%time
consolidate_metadata(Temp_2017, session=cache_session, concat_dim='time')

datacube has dimensions ['i[0:1:89]', 'j[0:1:89]', 'k[0:1:49]', 'tile[0:1:12]'] , and concat dim: `['time']`

CPU times: user 1.11 s, sys: 401 ms, total: 1.51 s
Wall time: 18.4 s

%%time
theta_salt_ds = xr.open_mfdataset(
    Temp_2017, 
    engine='pydap',
    session=cache_session, 
    parallel=True, 
    combine='nested', 
    concat_dim='time',
)

CPU times: user 281 ms, sys: 149 ms, total: 430 ms
Wall time: 371 ms

---------------------------------------------------------------------------
ParseError                                Traceback (most recent call last)
    [... skipping hidden 1 frame]

Cell In[21], line 1
----> 1 get_ipython().run_cell_magic('time', '', "theta_salt_ds = xr.open_mfdataset(\n    Temp_2017, \n    engine='pydap',\n    session=cache_session, \n    parallel=True, \n    combine='nested', \n    concat_dim='time',\n)\n")

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/interactiveshell.py:2565, in InteractiveShell.run_cell_magic(self, magic_name, line, cell)
   2564     args = (magic_arg_s, cell)
-> 2565     result = fn(*args, **kwargs)
   2567 # The code below prevents the output from being displayed
   2568 # when using magics with decorator @output_can_be_silenced
   2569 # when the last Python token in the expression is a ';'.

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/magics/execution.py:1452, in ExecutionMagics.time(self, line, cell, local_ns)
   1451 if exit_on_interrupt and captured_exception:
-> 1452     raise captured_exception
   1453 return

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/magics/execution.py:1416, in ExecutionMagics.time(self, line, cell, local_ns)
   1415 try:
-> 1416     exec(code, glob, local_ns)
   1417     out = None

File <timed exec>:1

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/xarray/backends/api.py:1812, in open_mfdataset(paths, chunks, concat_dim, compat, preprocess, engine, data_vars, coords, combine, parallel, join, attrs_file, combine_attrs, errors, **kwargs)
   1809 if parallel:
   1810     # calling compute here will return the datasets/file_objs lists,
   1811     # the underlying datasets will still be stored as dask arrays
-> 1812     datasets, closers = dask.compute(datasets, closers)
   1814 # Combine all datasets, closing them in case of a ValueError

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/dask/base.py:681, in compute(traverse, optimize_graph, scheduler, get, *args, **kwargs)
    679     keys = list(flatten(expr.__dask_keys__()))
--> 681     results = schedule(expr, keys, **kwargs)
    683 return repack(results)

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/xarray/backends/api.py:760, in open_dataset(filename_or_obj, engine, chunks, cache, decode_cf, mask_and_scale, decode_times, decode_timedelta, use_cftime, concat_characters, decode_coords, drop_variables, create_default_indexes, inline_array, chunked_array_type, from_array_kwargs, backend_kwargs, **kwargs)
    759 overwrite_encoded_chunks = kwargs.pop("overwrite_encoded_chunks", None)
--> 760 backend_ds = backend.open_dataset(
    761     filename_or_obj,
    762     drop_variables=drop_variables,
    763     **decoders,
    764     **kwargs,
    765 )
    766 ds = _dataset_from_backend_dataset(
    767     backend_ds,
    768     filename_or_obj,
   (...)    779     **kwargs,
    780 )

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/xarray/backends/pydap_.py:235, in PydapBackendEntrypoint.open_dataset(self, filename_or_obj, mask_and_scale, decode_times, concat_characters, decode_coords, drop_variables, use_cftime, decode_timedelta, group, application, session, output_grid, timeout, verify, user_charset)
    214 def open_dataset(
    215     self,
    216     filename_or_obj: (
   (...)    233     user_charset=None,
    234 ) -> Dataset:
--> 235     store = PydapDataStore.open(
    236         url=filename_or_obj,
    237         group=group,
    238         application=application,
    239         session=session,
    240         output_grid=output_grid,
    241         timeout=timeout,
    242         verify=verify,
    243         user_charset=user_charset,
    244     )
    245     store_entrypoint = StoreBackendEntrypoint()

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/xarray/backends/pydap_.py:131, in PydapDataStore.open(cls, url, group, application, session, output_grid, timeout, verify, user_charset)
    129 if isinstance(url, str):
    130     # check uit begins with an acceptable scheme
--> 131     dataset = open_url(**kwargs)
    132 elif hasattr(url, "ds"):
    133     # pydap dataset

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/pydap/client.py:156, in open_url(url, application, session, output_grid, timeout, verify, checksums, user_charset, protocol, batch, use_cache, session_kwargs, cache_kwargs, get_kwargs)
    150     session = create_session(
    151         use_cache=use_cache,
    152         session_kwargs=session_kwargs,
    153         cache_kwargs=cache_kwargs,
    154     )
--> 156 handler = DAPHandler(
    157     url,
    158     application,
    159     session,
    160     output_grid,
    161     timeout=timeout,
    162     verify=verify,
    163     checksums=checksums,
    164     user_charset=user_charset,
    165     protocol=protocol,
    166     get_kwargs=get_kwargs,
    167 )
    168 dataset = handler.dataset

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/pydap/handlers/dap.py:122, in DAPHandler.__init__(self, url, application, session, output_grid, timeout, verify, checksums, user_charset, protocol, get_kwargs)
    121 self.base_url = urlunparse(arg)
--> 122 self.make_dataset()
    123 self.add_proxies()

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/pydap/handlers/dap.py:157, in DAPHandler.make_dataset(self)
    156 if self.protocol == "dap4":
--> 157     self.dataset_from_dap4()
    158 else:

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/pydap/handlers/dap.py:186, in DAPHandler.dataset_from_dap4(self)
    185 dmr = safe_charset_text(r, self.user_charset)
--> 186 self.dataset = dmr_to_dataset(dmr)

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/pydap/parsers/dmr.py:252, in dmr_to_dataset(dmr)
    251 # Parse the DMR. First dropping the namespace
--> 252 dom_et = copy.deepcopy(DMRParser(dmr).node)
    253 # emtpy dataset

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/pydap/parsers/dmr.py:357, in DMRParser.__init__(self, dmr)
    356 _dmr = re.sub(' xmlns="[^"]+"', "", self.dmr, count=1)
--> 357 self.node = ET.fromstring(_dmr)
    358 if len(get_groups(self.node)) > 0:
    359     # no groups here

File ~/miniforge3/envs/pydap_docs/lib/python3.11/xml/etree/ElementTree.py:1350, in XML(text, parser)
   1349     parser = XMLParser(target=TreeBuilder())
-> 1350 parser.feed(text)
   1351 return parser.close()

ParseError: not well-formed (invalid token): line 1, column 0 (<string>)

During handling of the above exception, another exception occurred:

AssertionError                            Traceback (most recent call last)
    [... skipping hidden 1 frame]

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/interactiveshell.py:2164, in InteractiveShell.showtraceback(self, exc_tuple, filename, tb_offset, exception_only, running_compiled_code)
   2159     return
   2161 if issubclass(etype, SyntaxError):
   2162     # Though this won't be called by syntax errors in the input
   2163     # line, there may be SyntaxError cases with imported code.
-> 2164     self.showsyntaxerror(filename, running_compiled_code)
   2165 elif etype is UsageError:
   2166     self.show_usage_error(value)

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/interactiveshell.py:2254, in InteractiveShell.showsyntaxerror(self, filename, running_compiled_code)
   2252 # If the error occurred when executing compiled code, we should provide full stacktrace.
   2253 elist = traceback.extract_tb(last_traceback) if running_compiled_code else []
-> 2254 stb = self.SyntaxTB.structured_traceback(etype, value, elist)
   2255 self._showtraceback(etype, value, stb)

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/ultratb.py:1243, in SyntaxTB.structured_traceback(self, etype, evalue, etb, tb_offset, context)
   1241         value.text = newtext
   1242 self.last_syntax_error = value
-> 1243 return super(SyntaxTB, self).structured_traceback(
   1244     etype, value, etb, tb_offset=tb_offset, context=context
   1245 )

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/ultratb.py:212, in ListTB.structured_traceback(self, etype, evalue, etb, tb_offset, context)
    210     out_list.extend(self._format_list(elist))
    211 # The exception info should be a single entry in the list.
--> 212 lines = "".join(self._format_exception_only(etype, evalue))
    213 out_list.append(lines)
    215 # Find chained exceptions if we have a traceback (not for exception-only mode)

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/ultratb.py:341, in ListTB._format_exception_only(self, etype, value)
    327 output_list.append(
    328     theme_table[self._theme_name].format(
    329         [(Token, "  ")]
   (...)    336     )
    337 )
    338 if textline == "":
    339     # sep 2025:
    340     # textline = py3compat.cast_unicode(value.text, "utf-8")
--> 341     assert isinstance(value.text, str)
    342     textline = value.text
    344 if textline is not None:

AssertionError: 

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/async_helpers.py:128, in _pseudo_sync_runner(coro)
    120 """
    121 A runner that does not really allow async execution, and just advance the coroutine.
    122 
   (...)    125 Credit to Nathaniel Smith
    126 """
    127 try:
--> 128     coro.send(None)
    129 except StopIteration as exc:
    130     return exc.value

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/interactiveshell.py:3413, in InteractiveShell.run_cell_async(self, raw_cell, store_history, silent, shell_futures, transformed_cell, preprocessing_exc_tuple, cell_id)
   3409 exec_count = self.execution_count
   3410 if result.error_in_exec:
   3411     # Store formatted traceback and error details
   3412     self.history_manager.exceptions[exec_count] = (
-> 3413         self._format_exception_for_storage(result.error_in_exec)
   3414     )
   3416 # Each cell is a *single* input, regardless of how many lines it has
   3417 self.execution_count += 1

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/interactiveshell.py:3442, in InteractiveShell._format_exception_for_storage(self, exception, filename, running_compiled_code)
   3440     # Extract traceback if the error happened during compiled code execution
   3441     elist = traceback.extract_tb(tb) if running_compiled_code else []
-> 3442     stb = self.SyntaxTB.structured_traceback(etype, evalue, elist)
   3444 # Handle UsageError with a simple message
   3445 elif etype is UsageError:

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/ultratb.py:1243, in SyntaxTB.structured_traceback(self, etype, evalue, etb, tb_offset, context)
   1241         value.text = newtext
   1242 self.last_syntax_error = value
-> 1243 return super(SyntaxTB, self).structured_traceback(
   1244     etype, value, etb, tb_offset=tb_offset, context=context
   1245 )

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/ultratb.py:212, in ListTB.structured_traceback(self, etype, evalue, etb, tb_offset, context)
    210     out_list.extend(self._format_list(elist))
    211 # The exception info should be a single entry in the list.
--> 212 lines = "".join(self._format_exception_only(etype, evalue))
    213 out_list.append(lines)
    215 # Find chained exceptions if we have a traceback (not for exception-only mode)

File ~/miniforge3/envs/pydap_docs/lib/python3.11/site-packages/IPython/core/ultratb.py:341, in ListTB._format_exception_only(self, etype, value)
    327 output_list.append(
    328     theme_table[self._theme_name].format(
    329         [(Token, "  ")]
   (...)    336     )
    337 )
    338 if textline == "":
    339     # sep 2025:
    340     # textline = py3compat.cast_unicode(value.text, "utf-8")
--> 341     assert isinstance(value.text, str)
    342     textline = value.text
    344 if textline is not None:

AssertionError: 

theta_salt_ds

Finalmente, visualizamos THETA

Variable = [theta_salt_ds['THETA'][0, 0, i, :, :] for i in range(13)]
clevels = np.linspace(-5, 30, 100)
cMap='RdBu_r'

fig, axes = plt.subplots(nrows=4, ncols=4, figsize=(8, 8), gridspec_kw={'hspace':0.01, 'wspace':0.01})
AXES_NR = [
    axes[3, 0], axes[2, 0], axes[1, 0], axes[3, 1], axes[2, 1], axes[1, 1],
]
AXES_CAP = [axes[0, 0]]
AXES_R = [
    axes[1, 2], axes[2, 2], axes[3, 2], axes[1, 3], axes[2, 3], axes[3, 3],
]
for i in range(len(AXES_NR)):
    AXES_NR[i].contourf(Variable[i], clevels, cmap=cMap)

for i in range(len(AXES_CAP)):
    AXES_CAP[i].contourf(Variable[6].transpose()[:, ::-1], clevels, cmap=cMap)

for i in range(len(AXES_R)):
    AXES_R[i].contourf(Variable[7+i].transpose()[::-1, :], clevels, cmap=cMap)

for ax in np.ravel(axes):
    ax.axis('off')
    plt.setp(ax.get_xticklabels(), visible=False)
    plt.setp(ax.get_yticklabels(), visible=False)

plt.show()

Fig. 3. Visualizacion de la variable Surface temperature, similar al metodo utilizado en la Figura 2.